Applications of Queue Data StructureImagine a line forming at the desk of a movie theatre. A new individual join at the tail end of the line as the person in line who is first receives the ticket and departs. Queue Data Structure: What Is It?An ordered succession of elements is contained in a queue, which is a linear data structure. It is an abstract data type that resembles a stack partially. We can conduct operations on a queue's ends, unlike stacks, though. At one end of the queue, we add data, and at the other, we remove it. Imagine a line forming at the counter of a movie theatre. A new individual join at the tail end of the line as the person in line who is first receives the ticket and departs. The First In First Out principle, which controls how queues function, is based on this idea. 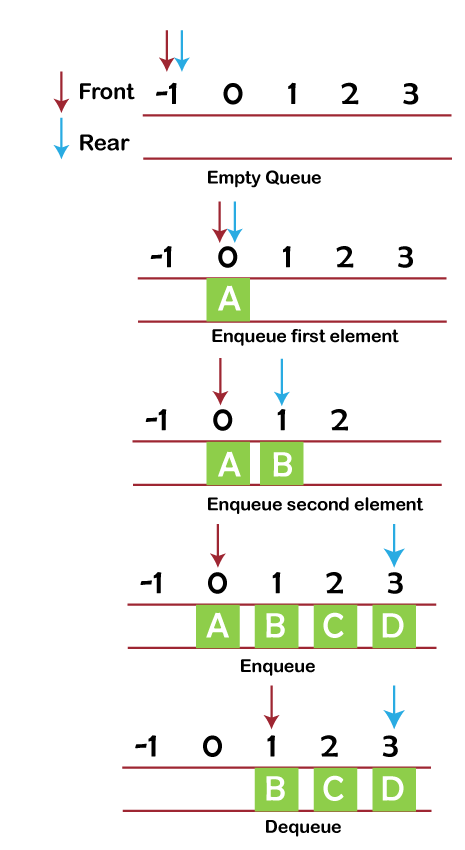 Basic Queue OperationsOn a queue, we can carry out the following actions:
We would have realised by now that two pointers are required for two distinct functions in a queue. The rear pointer points to the newly inserted element, while the front pointer is used to access or dequeue an element. How does a Queue Operate?The operations of a queue are as follows:
Operation EnqueueA complete queue should be checked.
Dispatch Operation
This will enable us to do the Dequeue Operation one at a time until we reset both points to 1, creating an empty queue. 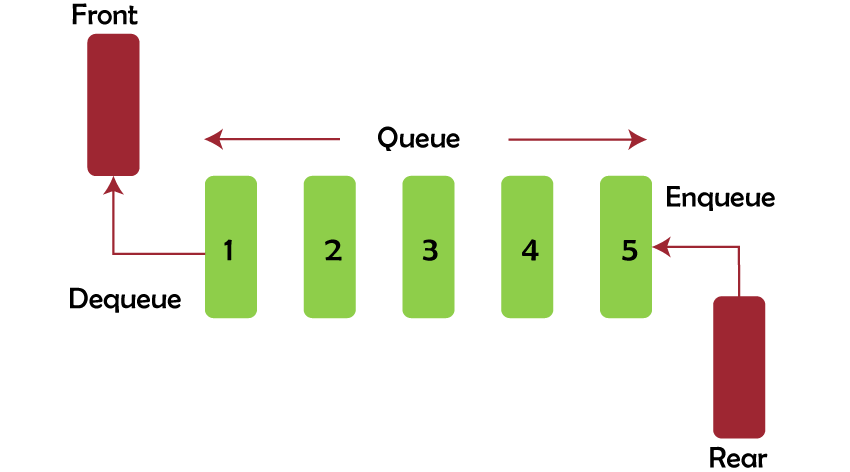 Next TopicLine Graph |

We provides tutorials and interview questions of all technology like java tutorial, android, java frameworks
G-13, 2nd Floor, Sec-3, Noida, UP, 201301, India












