Lagrange's Mean Value TheoremLagrange's mean value theorem is also known as the mean value theorem or MVT or LMVT. It states that if a function f (x) is a continuous in a close interval [a, b] where (a≤x ≤b) and differentiable in open interval [a, b] where (a < x< b), then there is at least one point x = c on this interval, given as f(b) - f (a) = f' (c) (b-a) The above theorem is called first mean value theorem. It enables to express the increment of a function in the given interval through the derivative value at an intermediate point of the segment. Proof of Lagrange's mean value theorem Consider the auxiliary function given below F (x) = f (x) + ?x Here, we will select a number ? so that the condition F (a) = F (b) is satisfied. Then 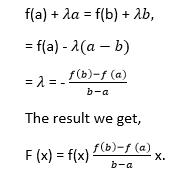 The function F (x) is continuous in the closed interval (a≤x ≤b), differentiable in the open interval (a < x< b), and takes equal values at the endpoints of the interval. So, it satisfies all the conditions of Rolle's theorem. Then, there is a point c exist in the interval (a,b) given as F' (c) = 0. It follows that 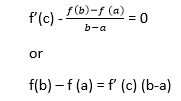 Let's understand this concept with the help of an example Example 1: Verify mean value theorem for f(x) = x2 in interval [4,6] Solution: Here, you need first to check out the function is continuous or not in the given closed interval; in our case, it is continuous. Then, you need to check the function is differentiable or not in the open interval (4,6); in our case, it is differentiable. F' (x) = 2x f(4) = 8 and f(6) = 36 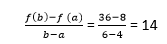 Mean value theorem states that there is a point c ε (4,6) such that f' (c) = 14. But, f' (x) = 2x which implies that c = 7. Thus at c = 7 ε (4,6), we have f' (c) = 14 Geometric InterpretationThe geometrical meaning of Lagrange's mean value theorem states that when the chord passing through the points of the graph corresponding to the ends of the segment a and b has the slope equals to 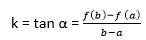 then there is a point x = c located inside the interval [a,b], where the tangent to the graph is parallel to the chord. 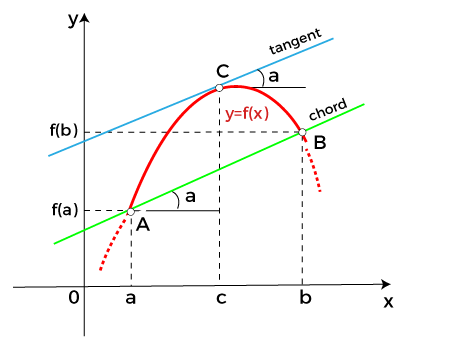 Physical InterpretationLagrange's mean value theorem has a very clear physical interpretation. Let's consider that f(p) represents the position of an object moving along a line, depending on the time p. The ratio of Lagrange's mean value theorem has broad applications in mathematical analysis, computational mathematics and other fields. Let us consider two different results. Output 1 In a specific case when the values of the function f (x) at the endpoints of the segment [a,b] are equal that is f(a) = f (b), then the mean value theorem implies that there is a point c ε (a,b) such that f'(c) - We get Rolle's theorem, which can be considered a special case of Lagrange's mean value theorem. Output 2 If the derivative f' (x) is null at all points in the interval [a,b], the function f (x) is constant on this interval. Undoubtably, for any two points p1 and p2 in the interval [a,b], there exists a point c ε (a,b), such that f(p2)- f (p1) = f' (c) (p2 - p1) = 0. (x2-x1) = 0 Consequently F(p1) = f (p2) Questions based on Lagrange's mean value theoremExample 1: A thermometer was taken from the deep freezer and placed in hot water. It took 30 sec for the thermometer to rise from -5 degrees Celsius to 100 degrees Celsius. Find the average rate of temperature change. Solution: Given; T (t1) = -5 T (t2) = 100 And t2 - t1 = 30 0C As we know, The average rate of temperature change 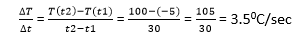 Example 2: Check the validity of Lagrange's mean value theorem for the function f(x) = (x2 - 2x + 3) on the interval [1, 2]. If the theorem holds, determine a point x satisfying the conditions of the theorem. Solution: The given quadratic equation is continuous and differentiable on the entire set of real numbers. Therefore, we can apply Lagrange's mean value theorem in the given equation. The derivative of the function has the form F'(x) = (x2 - 2x + 3) = 2x - 2 Determine the coordinates of the point c: 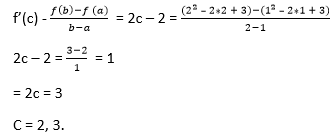 You can see that the point c = 2,3 lies in the interval (1,2) Example 3: The position of an object is given by the function s (t) = t2 +5t - 6. Determine the time t = c in the interval 0 ≤t ≤6 when the object's instantaneous velocity is equal to its average velocity in this interval. Solution: The given function s (t) satisfies the mean value theorem principle, so we can write 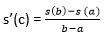 where, s = 0, and b = 6 taking the derivative: s'(x) = (t2 +5t -6)' = 2t + 5 substituting this equation we get, 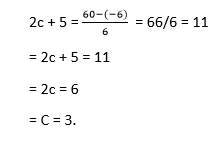 Next TopicCauchy's Mean Value Theorem |