NCERT Solutions Class 11th Maths Chapter 1: SetsExercise 1.11. Which of the following are sets? Justify your answer.
SOLUTION
2. Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank spaces: (i) 5. . .A (ii) 8 . . . A (iii) 0. . .A (iv) 4. . . A (v) 2. . .A (vi) 10. . .A SOLUTION
3. Write the following sets in roster form:
SOLUTION (i) Integers greater than -3 and smaller than 7 are -2, -1, 0, 1, 2, 3, 4, 5, 6. Therefore, A = {-2, -1, 0, 1, 2, 3, 4, 5, 6} (ii) Natural numbers less than 6 are 1, 2, 3, 4, 5 Therefore, B = {1, 2, 3, 4, 5} (iii) Two-digit numbers whose digits add up to 8 are 17, 26, 35, 44, 53, 62, 71, 80. Therefore, C = {17, 26, 35, 44, 53, 62, 71, 80} (iv) We know that, 60 = 2 × 2 × 3 × 5 Prime numbers that are divisors of 60 are 2, 3, 5. Therefore, D = {2, 3, 5} (v) All unique letters in the word TRIGONOMETRY are T, R, I, G, O, N, M, E, Y. Therefore, E = {T, R, I, G, O, N, M, E, Y} (vi) All unique letters in the word BETTER are B, E, T, R. Therefore, F = {B, E, T, R} 4. Write the following sets in the set-builder form : (i) (3, 6, 9, 12} (ii) {2,4,8,16,32} (iii) {5, 25, 125, 625} (iv) {2, 4, 6, . . .} (v) {1,4,9, . . .,100} SOLUTION (i) It can be observed that the elements of this set are multiples of 3. Therefore, it can be written as {x: x = 3n, where n ∈ N and 1 ≤n ≤ 4} (ii) It can be observed that the elements of this set are two times that of their respective previous ones. Therefore, it can be written as {x: x = 2n, where n ∈ N and 1 ≤ n ≤ 5} (iii) It can be observed that the elements of this set are five times that of their respective previous ones. Therefore, it can be written as {x: x = 5n, where n ∈ N and 1 ≤ n ≤ 4} (iv) It can be observed that the elements of this set are even natural numbers. Therefore, it can be written as {x: x is an even natural number} (v) It can be observed that the elements of this set are in the series 12, 22, 32 and so on upto 102. Therefore, it can be written as {x: x = n2, where n ∈ N and 1 ≤ n ≤ 10} 5. List all the elements of the following sets:
SOLUTION (i) Odd natural numbers are 1, 3, 5, 7, ... and so on. Therefore, A = {1, 3, 5, 7, ...} (ii) Integers between -1/2 and 9/2 will be 0, 1, 2, 3, 4. Therefore, B = {0, 1, 2, 3, 4} (iii) Integers whose squares are less than or equal to 4 include -2, -1, 0, 1, 2. Therefore, C = {-2, -1, 0, 1, 2} (iv) The unique letters in the word LOYAL are L, O, Y, A. Therefore, D = {L, O, Y, A} (v) Months of the year not having 31 days are February, April, June, September, November. Therefore, E = {February, April, June, September, November} (vi) Consonants of the English alphabet that occur before k are b, c, d, f, g, h, j. Therefore, F = {b, c, d, f, g, h, j} 6. Match each of the set on the left in the roster form with the same set on the right described in set-builder form: (i) {1, 2, 3, 6} (a) {x : x is a prime number and a divisor of 6} (ii) {2, 3} (b) {x : x is an odd natural number less than 10} (iii) {M,A,T,H,E,I,C,S} (c) {x : x is natural number and divisor of 6} (iv) {1, 3, 5, 7, 9} (d) {x : x is a letter of the word MATHEMATICS}. SOLUTION
Exercise 1.21. Which of the following are examples of the null set
SOLUTION
2. Which of the following sets are finite or infinite
SOLUTION
3. State whether each of the following set is finite or infinite:
SOLUTION
4. In the following, state whether A = B or not:
SOLUTION
5. Are the following pair of sets equal ? Give reasons.
SOLUTION (i) First, we need to find the solution of x2 + 5x + 6 = 0. x2 + 5x + 6 = 0 x2 + 2x + 3x + 6 = 0 x(x + 2) + 3(x + 2) = 0 (x + 2)(x + 3) = 0 x = -2 and x = -3. Thus, B = {-2, -3}. -2 ∉ A and -3 ∉ A. Hence, A ≠ B. (ii) Letters in the word FOLLOW are F, O, L, W. Thus, A = {F, O, L, W} Letters in the word WOLF are W, O, L, F. Thus, B = {W, O, L, F} All elements of A are present in B and all elements of B are present in A. Hence, A = B. 6. From the sets given below, select equal sets : A = { 2, 4, 8, 12}, B = { 1, 2, 3, 4}, C = { 4, 8, 12, 14}, D = { 3, 1, 4, 2} E = {-1, 1}, F = { 0, a}, G = {1, -1}, H = { 0, 1} SOLUTION All elements of B are present in D and all elements of D are present in A. Therefore, B = D. All elements of E are present in G and all elements of G are present in E. Therefore, E = G. None of the other sets have all their elements present in the other. Exercise 1.31. Make correct statements by filling in the symbols ⊂ or ⊄ in the blank spaces :
SOLUTION
2. Examine whether the following statements are true or false:
SOLUTION
Hence, the statement is true. 3. Let A = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why? (i) {3, 4} ⊂ A (ii) {3, 4} ∈ A (iii) {{3, 4}} ⊂ A (iv) 1 ∈ A (v) 1 ⊂ A (vi) {1, 2, 5} ⊂ A (vii) {1, 2, 5} ∈ A (viii) {1, 2, 3} ⊂ A (ix) φ ∈ A (x) φ ⊂ A (xi) {φ} ⊂ A SOLUTION
4. Write down all the subsets of the following sets
SOLUTION
5. How many elements has P(A), if A = φ? SOLUTION Let m be the number of elements in the set A. Now, n(A) = m. Therefore, n[P(A)] = 2m It is given that A = φ. So, n(A) = m = 0 n[P(A)] = 20 = 1 Hence, P(A) has 1 element. 6. Write the following as intervals : (i) {x : x ∈ R, - 4 < x ≤ 6} (ii) {x : x ∈ R, - 12 < x < -10} (iii) {x : x ∈ R, 0 ≤ x < 7} (iv) {x : x ∈ R, 3 ≤ x ≤ 4} SOLUTION
7. Write the following intervals in set-builder form : (i) (- 3, 0) (ii) [6 , 12] (iii) (6, 12] (iv) [-23, 5) SOLUTION
8. What universal set(s) would you propose for each of the following : (i) The set of right triangles. (ii) The set of isosceles triangles. SOLUTION
9. Given the sets A = {1, 3, 5}, B = {2, 4, 6} and C = {0, 2, 4, 6, 8}, which of the following may be considered as universal set (s) for all the three sets A, B and C
SOLUTION
Exercise 1.41. Find the union of each of the following pairs of sets :
SOLUTION (i) X ∪ Y = {1, 2, 3, 5} A ∪ B = {a, b, c, e, i, o , u} (iiI) A = {3, 6, 9, ...} B = {1, 2, 3, 4, 5} A ∪ B = {1, 2, 3, 4, 5, 6, 9, 12, ...} (iv) A = {2, 3, 4, 5, 6} B = {7, 8, 9} A ∪ B = {2, 3, 4, 5, 6, 7, 8, 9} (v) A ∪ B = {1, 2, 3} 2. Let A = { a, b }, B = {a, b, c}. Is A ⊂ B ? What is A ∪ B ? SOLUTION Each element of the set A is present in set B. Therefore, A ⊂ B. A ∪ B = {a, b, c} = B as A is the subset of B. 3. If A and B are two sets such that A ⊂ B, then what is A ∪ B ? SOLUTION If A ⊂ B, then A ∪ B will be the same as set B as it is the superset. 4. If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 }and D = { 7, 8, 9, 10 }; find (i) A ∪ B (ii) A ∪ C (iii) B ∪ C (iv) B ∪ D (v) A ∪ B ∪ C (vi) A ∪ B ∪ D (vii) B ∪ C ∪ D SOLUTION
5. Find the intersection of each pair of sets of question 1 above. [Pairs of Sets From Question 1:
SOLUTION (i) X ∩ Y = {1, 3} (ii) A ∩ B = {a} (iiI) A = {3, 6, 9, ...} B = {1, 2, 3, 4, 5} A ∩ B = {3} (iv) A = {2, 3, 4, 5, 6} B = {7, 8, 9} A ∩ B = φ (v) A ∩ B = φ 6. If A = { 3, 5, 7, 9, 11 }, B = {7, 9, 11, 13}, C = {11, 13, 15}and D = {15, 17}; find (i) A ∩ B (ii) B ∩ C (iii) A ∩ C ∩ D (iv) A ∩ C (v) B ∩ D (vi) A ∩ (B ∪ C) (vii) A ∩ D (viii) A ∩ (B ∪ D) (ix) ( A ∩ B ) ∩ ( B ∪ C ) (x) ( A ∪ D) ∩ ( B ∪ C) SOLUTION
7. If A = {x : x is a natural number }, B = {x : x is an even natural number} C = {x : x is an odd natural number} and D = {x : x is a prime number }, find (i) A ∩ B (ii) A ∩ C (iii) A ∩ D (iv) B ∩ C (v) B ∩ D (vi) C ∩ D SOLUTION A = {1, 2, 3, 4, ...} B = {2, 4, 6, 8, ...} C = {1, 3, 5, 7, ...} D = {2, 3, 5, 7, ...}
8. Which of the following pairs of sets are disjoint
SOLUTION (i) {x:xis a natural number and 4≤x≤6} = {4, 5, 6} {1, 2, 3, 4} ∩ {4, 5, 6} = {4} Since, the intersection of the two sets is not φ. Therefore, the given pair of sets are not disjoint. (ii) {a, e, I, o, u} ∩ {c, d, e, f} = {e} Since, the intersection of the two sets is not φ. Therefore, the given pair of sets are not disjoint. (iii) {x : x is an even integer} = {..., -4, -2, 0, 2, 4, ...} {x : x is an odd integer} = {..., -3, -1, 1, 3, ...} {..., -4, -2, 0, 2, 4, ...} ∩ {..., -3, -1, 1, 3, ...} = φ Since, the intersection of the two sets is φ. Therefore, the given pair of sets are disjoint. 9. If A = {3, 6, 9, 12, 15, 18, 21}, B = { 4, 8, 12, 16, 20 }, C = { 2, 4, 6, 8, 10, 12, 14, 16 }, D = {5, 10, 15, 20 }; find (i) A - B (ii) A - C (iii) A - D (iv) B - A (v) C - A (vi) D - A (vii) B - C (viii) B - D (ix) C - B (x) D - B (xi) C - D (xii) D - C SOLUTION
10. If X = { a, b, c, d } and Y = { f, b, d, g}, find (i) X - Y (ii) Y - X (iii) X ∩ Y SOLUTION
11. If R is the set of real numbers and Q is the set of rational numbers, then what is R - Q? SOLUTION The set of real numbers is broadly made up of rational and irrational numbers. Therefore, R - Q will be the set of irrational numbers. 12. State whether each of the following statement is true or false. Justify your answer.
SOLUTION (i) {2, 3, 4, 5} ∩ {3, 6} = {3} Since, the intersection of the two sets is not φ. Therefore, the given pair of sets are not disjoint. Hence, the statement is false. (ii) {a, e, i, o, u} ∩ {a, b, c, d} = {a} Since, the intersection of the two sets is not φ. Therefore, the given pair of sets are not disjoint. (iii) {2, 6, 10, 14} ∩ {3, 7, 11, 15} = φ Since, the intersection of the two sets is φ. Therefore, the given pair of sets are disjoint. (iv) {2, 6, 10} ∩ {3, 7, 11} = φ Since, the intersection of the two sets is φ. Therefore, the given pair of sets are disjoint. Exercise 1.51. Let U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }, A = { 1, 2, 3, 4}, B = { 2, 4, 6, 8 } and C = { 3, 4, 5, 6 }. Find
SOLUTION (i) A' = {5, 6, 7, 8, 9} (ii) B' = {1, 3, 5, 7, 9} (iii) A U C = {1, 2, 3, 4, 5, 6} (A U C)' = {7, 8, 9} (iv) A U B = {1, 2, 3, 4, 6, 8} (A U B)' = {5, 7, 9} (v) (A')' = A = {1, 2, 3, 4} (vi) B - C = {2, 8} (B - C)' = {1, 3, 4, 5, 6, 7, 9} 2. If U = { a, b, c, d, e, f, g, h}, find the complements of the following sets : (i) A = {a, b, c} (ii) B = {d, e, f, g} (iii) C = {a, c, e, g} (iv) D = { f, g, h, a} SOLUTION (i)A = {a, b, c} A' = {d, e, f, g, h} (ii)B = {d, e, f, g} B' = {a, b, c, h} (iii)C = {a, c, e, g} C' = {b, d, f, h} (iv)D = {f,g,h,a} D' = {b, c, d, e} 3. Taking the set of natural numbers as the universal set, write down the complements of the following sets: (i) {x : x is an even natural number} (ii) { x : x is an odd natural number } (iii) {x : x is a positive multiple of 3} (iv) { x : x is a prime number } (v) {x : x is a natural number divisible by 3 and 5} (vi) { x : x is a perfect square } (vii) { x : x is a perfect cube} (viii) { x : x + 5 = 8 } (ix) { x : 2x + 5 = 9} (x) { x : x ≥ 7 } (xi) { x : x ∈ N and 2x + 1 > 10 } SOLUTION (i) {x : x is an even natural number} = {2, 4, 6, 8, ...} {2, 4, 6, 8, ...}' = {1, 3, 5, 7, ...} = {x : x is an odd natural number} (ii) {x : x is an odd natural number} = {1, 3, 5, 7, ...} {1, 3, 5, 7, ...}' = {2, 4, 6, 8, ...} = {x : x is an even natural number} (iii) {x : x is a positive multiple of 3} = {3, 6, 9, 12, ...} {3, 6, 9, 12, ...}' = {1, 2, 4, 5, 7, 8, ...} = {x : x is not a multiple of 3} (iv) {x : x is a prime number} = {2, 3, 5, 7, ...} {2, 3, 5, 7, ...}' = {1, 4, 6, 8, ...} = {x : x is a composite number or x = 1} (v) {x : x is a natural number divisible by 3 and 5} = {15, 30, 45, 60, ...} {15, 30, 45, 60, ...}' = {1, 2, 3, 4, ..., 13, 14, 16, ...} = {x : x is a natural number not divisible by 3 or 5} (vi) {x : x is a perfect square} = {1, 4, 9, 16, ...} {1, 4, 9, 16, ...}' = {2, 3, 5, 6, ...} = {x : x is not a perfect square} (vii) {x : x is a perfect cube} = {1, 8, 27, 64, ...} {1, 8, 27, 64, ...}' = {2, 3, 4, 5, 6, 7, 9, ...} (viii) x + 5 = 8 x = 3 {x : x + 5 = 8}' = {x : x ∈ N where x ≠ 3} (ix) 2x + 5 = 9 2x = 4 x = 2 {x : 2x + 5 = 9}' = {x : x ∈ N where x ≠ 2} (x) {x : x ≥ 7}' = {x : x < 7} (xi) 2x + 1 > 10 2x > 9 x > 9/2 {x :x∈ N and 2x+ 1 > 10}� = {x:x∈ N wherex≤ 9/2} 4. If U = {1, 2, 3, 4, 5, 6, 7, 8, 9 }, A = {2, 4, 6, 8} and B = { 2, 3, 5, 7}. Verify that (i) (A ∪ B)? = A? ∩ B? (ii) (A ∩ B)? = A? ∪ B? SOLUTION (i) LHS = (A ∪ B)' = {2, 3, 4, 5, 6, 7, 8}' = {1, 9} RHS = A' ∩ B' = {1, 3, 5, 7, 9} ∩ {1, 4, 6, 8, 9} = {1, 9} LHS = RHS. Hence, verified. (ii) LHS = (A ∩ B)' = {2}' = {1, 3, 4, 5, 6, 7, 8, 9} RHS = A' ∪ B' = {1, 3, 5, 7, 9} ∪ {1, 4, 6, 8, 9} = {1, 3, 4, 5, 6, 7, 8, 9} LHS = RHS. Hence, verified. 5. Draw appropriate Venn diagram for each of the following : (i) (A ∪ B)?, (ii) A? ∩ B?, (iii) (A ∩ B)?, (iv) A? ∪ B? SOLUTION (i) 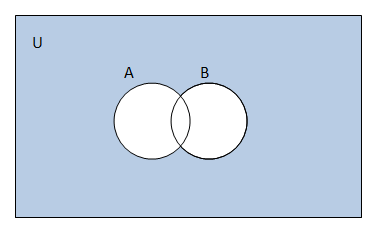 (ii) 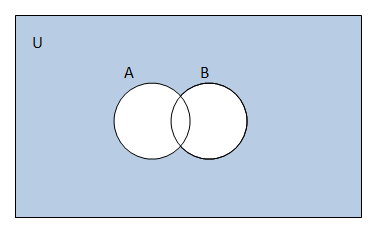 (iii) 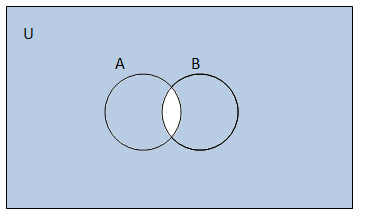 (iv) 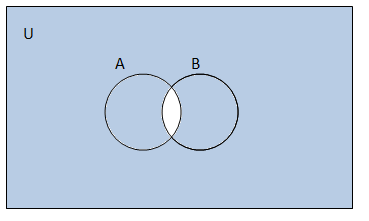 6. Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from 60�, what is A?? SOLUTION A is the set of all triangles with at least one angle different from 60�. Then, A' will be the set of all triangles with no angle different from 60�. Hence, A' will be the set of all equilateral triangles. 7. Fill in the blanks to make each of the following a true statement : (i) A ∪ A? = . . . (ii) φ? ∩ A = . . . (iii) A ∩ A? = . . . (iv) U? ∩ A = . . . SOLUTION
Exercise 1.61. If X and Y are two sets such that n ( X ) = 17, n ( Y ) = 23 and n ( X ∪ Y ) = 38, find n ( X ∩ Y ). SOLUTION We know that n (X U Y) = n (X) + n (Y) - n (X ∩ Y) 38 = 17 + 23 - n (X ∩ Y) 38 = 40 - n (X ∩ Y) -2 = -n (X ∩ Y) n (X ∩ Y) = 2 2. If X and Y are two sets such that X ∪ Y has 18 elements, X has 8 elements and Y has 15 elements ; how many elements does X ∩ Y have? SOLUTION We know that n (X U Y) = n (X) + n (Y) - n (X ∩ Y) 18 = 8 + 15 - n (X ∩ Y) 18 = 23 - n (X ∩ Y) -5 = -n (X ∩ Y) n (X ∩ Y) = 5 3. In a group of 400 people, 250 can speak Hindi and 200 can speak English. How many people can speak both Hindi and English? SOLUTION Let the set of people who can speak hindi be X and let the set of people who can speak English be Y. n (X) = 250 n (Y) = 200 n (X ∪ Y) = 400 We know that n (X U Y) = n (X) + n (Y) - n (X ∩ Y) 400 = 250 + 200 - n (X ∩ Y) 400 = 450 - n (X ∩ Y) -50 = -n (X ∩ Y) n (X ∩ Y) = 50 Hence, 50 people can speak both Hindi and English. 4. If S and T are two sets such that S has 21 elements, T has 32 elements, and S ∩ T has 11 elements, how many elements does S ∪ T have? SOLUTION We know that n (S U T) = n (S) + n (T) - n (S ∩ T) n (S U T) = 21 + 32 - 11 n (S ∪ T) = 42 5. If X and Y are two sets such that X has 40 elements, X ∪ Y has 60 elements and X ∩ Y has 10 elements, how many elements does Y have? SOLUTION We know that n (X U Y) = n (X) + n (Y) - n (X ∩ Y) 60 = 40 + n (Y) - 10 60 = 30 + n (Y) n (Y) = 30 6. In a group of 70 people, 37 like coffee, 52 like tea and each person likes at least one of the two drinks. How many people like both coffee and tea? SOLUTION Let the set of people who like coffee be X and let the set of people who like tea be Y. n (X) = 37 n (Y) = 52 n (X ∪ Y) = 70 We know that n (X U Y) = n (X) + n (Y) - n (X ∩ Y) 70 = 37 + 52 - n (X ∩ Y) 70 = 89 - n (X ∩ Y) -19 = -n (X ∩ Y) n (X ∩ Y) = 19 Hence, 19 people like both tea and coffee. 7. In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. How many like tennis only and not cricket? How many like tennis? SOLUTION Let the set of people who like cricket be X and let the set of people who like tennis be Y. n (X) = 40 n (X ∪ Y) = 65 n (X ∩ Y) = 10 We know that n (X U Y) = n (X) + n (Y) - n (X ∩ Y) 65 = 40 + n (Y) - 10 65 = 30 + n (Y) n (Y) = 35 Therefore, 35 people like tennis. Number of people who like tennis only and not cricket = n (Y - X) n (Y - X) = n (Y) - n (X ∩ Y) n (Y - X) = 35 - 10 = 25 Hence, 25 people like only tennis and not cricket, whereas 35 people like tennis. 8. In a committee, 50 people speak French, 20 speak Spanish and 10 speak both Spanish and French. How many speak at least one of these two languages? SOLUTION Let the set of people who can speak French be X and let the set of people who can speak Spanish be Y. n (X) = 50 n (Y) = 20 n (X ∩ Y) = 10 We know that n (X U Y) = n (X) + n (Y) - n (X ∩ Y) n (X U Y) = 50 + 20 - 10 n (X ∪ Y) = 60 Hence, 60 people can speak at least one of the two languages. Miscellaneous Exercise1. Decide, among the following sets, which sets are subsets of one and another: A = { x : x ∈ R and x satisfy x2 - 8x + 12 = 0 }, B = { 2, 4, 6 }, C = { 2, 4, 6, 8, . . . }, D = { 6 }. SOLUTION x2 - 8x + 12 = 0 x2 - 6x - 2x + 12 = 0 x(x - 6) - 2(x - 6) = 0 (x - 6)(x - 2) = 0 x = 6 and x = 2. Therefore, A = {2, 6}. Now, B = {2, 4, 6 }, C = {2, 4, 6, 8, . . . }, and D = {6}. Hence, we can conclude: D ⊂ A, D ⊂ B, D ⊂ C, A ⊂ B, A ⊂ C B ⊂ C 2. In each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.
SOLUTION (i) This statement is false. Let us assume that A = {1, 2, 3} and B = {{1, 2, 3}, 4} Here, 1 ∈ A and A ∈ B. However, 1 ∉ B. (ii) This statement is false. Let us assume that A = {1, 2}, B = {1, 2, 3} and C = {{1, 2, 3}, 4} Here, A ⊂ B and B ∈ C. However, A ∉ C. (iii) This statement is true. It is given that A ⊂ B and B ⊂ C. Therefore, For any element x of the set A: x ∈ A, then x ∈ B and x ∈ C. Thus, A ⊂ C. (iv) This statement is false. Let us assume that A = {1, 2}, B = {3, 4} and C = {1, 2, 3}. Here, A ⊄ B and B ⊄ C. However, A ⊂ C. (v) This statement is false. Let us assume that A = {1, 2, 3} and B = {4, 5, 6}. Here, 1 ∈ A and A ⊄ B. However, 1 ∉ B. (vi) This statement is true. It is given that A ⊂ B and x ∉ B. If x ∈ A is true, then x ∈ B is also true as A ⊂ B. But x ∉ B. Hence, x ∉ A. 3. Let A, B, and C be the sets such that A ∪ B = A ∪ C and A ∩ B = A ∩ C. Show that B = C. SOLUTION If x ∈ B for any element x, then x ∈ A ∪ B Since, A ∪ B = A ∪ C. Therefore, x ∈ A ∪ C This means that either set A or set C have x. If x ∈ A, then x ∈ A ∩ B as x ∈ B. Since, A ∩ B = A ∩ C. Therefore, x ∈ A ∩ C This means that set C has x. Since, x ∈ B and x ∈ C. Therefore, B ⊂ C. Similarly, C ⊂ B. Since, B ⊂ C and C ⊂ B. Hence, B = C. 4. Show that the following four conditions are equivalent : (i) A ⊂ B (ii) A - B = φ (iii) A ∪ B = B (iv) A ∩ B = A SOLUTION Equivalence in (i) and (ii): Let A ⊂ B be true. Now, let us assume that A - B ≠ φ. This means that, an element x exists such that x ∈ A and x ∉ B. But this is not possible as A ⊂ B, so every element in A has to be in B. Therefore, A - B = φ Hence, (i) and (ii) conditions are equivalent. Equivalence in (i) and (iii): Let A ⊂ B be true. We know that, B ⊂ A ∪ B. For any element x of the set A ∪ B, we have x ∈ A ∪ B So, x ∈ A or x ∈ B. I. If x ∈ A, then x ∈ B because A ⊂ B. So, A ∪ B ⊂ B II. If x ∈ B, then A ∪ B = B as B is the superset. Now, let us assume that A ∪ B = B. If x ∈ A, then x ∈ A ∪ B because clearly A ⊂ A ∪ B. and x ∈ B because A ∪ B = B. Therefore, A ⊂ B. Hence, (i) and (iii) conditions are equivalent. Equivalence in (i) and (iv): Let A ⊂ B be true. A ∩ B ⊂ A If x ∈ A then x ∈ B as A ⊂ B. So, x ∈ A ∩ B This means that A ⊂ A ∩ B. Since, A ∩ B ⊂ A and A ⊂ A ∩ B. Therefore, A = A ∩ B. Now, let us assume that A ∩ B = B. If x ∈ A, then x ∈ A ∩ B So, x is an element of A as well as B. x ∈ A and x ∈ B. Therefore, A ⊂ B. Hence, (i) and (iv) conditions are equivalent. Hence, (i), (ii), (iii), and (iv) conditions are all equivalent. 5. Show that if A ⊂ B, then C - B ⊂ C - A. SOLUTION Let there be an element x in the set C - B. This means that x ∈ C and x ∉ B. Since, A ⊂ B. Therefore, x ∈ C and x ∉ A. This implies that x ∈ C - A. Hence, C - B ⊂ C - A. 6. Assume that P ( A ) = P ( B ). Show that A = B. SOLUTION Let there be an element x in the set A. We know that P (A) contains all the subsets of set A. So, A ∈ P (A). P (A) = P (B) Thus, A ∈ P (B) Let there be a subset C of the set B such that x ∈ C. We know that P (B) contains all the subsets of set B. So, C ∈ P (B). This implies that C ⊂ B. Therefore, x ∈ B which further implies that A ⊂ B. Similarly, we can prove that B ⊂ A. Hence, A = B. 7. Is it true that for any sets A and B, P ( A ) ∪ P ( B ) = P ( A ∪ B )? Justify your answer. SOLUTION The given statement is false for any sets A and B. P (A) ∪ P (B) ≠ P (A ∪ B) Let us assume that there are two sets A = {1, 2, 3} and B = {3, 4, 5}. A ∪ B = {1, 2, 3, 4, 5} P (A) = {φ, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, {1, 2, 3}} P (B) = {, {3}, {4}, {5}, {3, 4}, {4, 5}, {3, 5}, {3, 4, 5}} LHS = P (A) ∪ P (B) = {φ, {1}, {2}, {3}, {4}, {5}, {1, 2}, {2, 3}, {1, 3}, {3, 4}, {4, 5}, {3, 5}, {1, 2, 3}, {3, 4, 5}} RHS = P (A ∪ B) = {φ, {1}, {2}, {3}, {4}, {5}, {1, 2}, {2, 3}, {3, 4}, {4, 5}, {1, 3}, {1, 4}, {1, 5}, {2, 4}, {2, 5}, {3, 5}, {1, 2, 3}, {2, 3, 4}, {3, 4, 5}, {1, 2, 4}, {1, 2, 5}, {1, 3, 4}, {1, 3, 5}, {1, 4, 5}, {2, 3, 5}, {2, 4, 5}, {1, 2, 3, 4}, {2, 3, 4, 5}, {1, 2, 3, 5}, {1, 3, 4, 5}, {1, 2, 4, 5}, {1, 2, 3, 4, 5}} LHS ≠ RHS. Hence, proved that the given statement is not true. 8. Show that for any sets A and B, A = ( A ∩ B ) ∪ ( A - B ) and A ∪ ( B - A ) = ( A ∪ B ) SOLUTION Let there be an element x such that x ∈ A. CASE I: If x ∈ A ∩ B Then, x ∈ (A ∩ B) ⊂ (A ∪ B) ∪ (A - B) CASE II: If x ∉ A ∩ B Then, Either x ∉ A or x ∉ B. But we know that x ∈ A. Thus, x ∉ B x ∉ (A - B) ⊂ (A ∪ B) ∪ (A - B) Therefore, A ⊂ (A ∩ B) ∪ (A - B) Since, A ∩ B ⊂ A and (A - B) ⊂ A. Then, (A ∩ B) ∪ (A - B) ⊂ A From the above two obtained statements, we can conclude that A = (A ∩ B) ∪ (A - B) The first statement has been proven. Now, let us assume that x ∈ A ∪ (B - A). This implies that x ∈ A or x ∈ (B - A) x ∈ A or [x ∈ B and x ∉ A] x ∈ B ∪ A Therefore, A ∪ (B - A) ⊂ (A ∪ B) Let there be an element y such that y ∈ A ∪ B y ∈ A or y ∈ B y ∈ A or [y ∈ B and y ∉ A] y ∈ A ∪ (B - A) Therefore, A ∪ B ⊂ A ∪ (B - A) From the above two obtained statements, we can conclude that A ∪ (B - A) = (A ∪ B) Hence, both the required statements have been proven. 9. Using properties of sets, show that (i) A ∪ ( A ∩ B ) = A (ii) A ∩ ( A ∪ B ) = A SOLUTION (i) It is obvious that A ⊂ A. Then, A ∩ B ⊂ A A ∪ (A ∩ B) ⊂ A Also, A ⊂ A ∪ (A ∩ B) Therefore, A = A ∪ (A ∩ B) (ii) A ∩ (A ∪ B) = (A ∩ A) ∪ (A ∩ B) = A ∪ (A ∩ B) = A Therefore, A = A ∪ (A ∩ B) 10. Show that A ∩ B = A ∩ C need not imply B = C. SOLUTION Let us assume that there are three sets A = {1, 2}, B = {1, 3, 4} and C = {1, 5, 6}. Now, A ∩ B = {1} A ∩ C = {1} Therefore, A ∩ B = A ∩ C 3 and 4 ∈ B but 3 and 4 ∉ C. Hence, B ≠ C. 11. Let A and B be sets. If A ∩ X = B ∩ X = φ and A ∪ X = B ∪ X for some set X, show that A = B. (Hints A = A ∩ ( A ∪ X ) , B = B ∩ ( B ∪ X ) and use Distributive law ) SOLUTION To Prove: A = B Proof: A = A ∩ (A ∪ X) = A ∩ (B ∪ X) [A ∪ X = B ∪ X] A = (A ∩ B) ∪ (A ∩ X) (Using the Distributive law) A = (A ∩ B) ∪ Φ [A ∩ X = Φ] A = A ∩ B ... (I) Now, B = B ∩ (B ∪ X) B = B ∩ (A ∪ X) [A ∪ X = B ∪ X] B = (B ∩ A) ∪ (B ∩ X) (Using the Distributive law) B = (B ∩ A) ∪ Φ [B ∩ X = Φ] B = A ∩ B ... (II) From Equations (I) and (II) A = B Hence, proved. 12. Find sets A, B and C such that A ∩ B, B ∩ C and A ∩ C are non-empty sets and A ∩ B ∩ C = φ. SOLUTION Let there be three sets A = {1, 2}, B = {2, 3}, and C = {1, 3}. A ∩ B = {2} B ∩ C = {3} A ∩ C = {1} A ∩ B ∩ C = φ Therefore, sets A = {1, 2}, B = {2, 3} and C = {1, 3} are example of three sets such that A ∩ B, B ∩ C and A ∩ C are non-empty sets and A ∩ B ∩ C = φ. 13. In a survey of 600 students in a school, 150 students were found to be taking tea and 225 taking coffee, 100 were taking both tea and coffee. Find how many students were taking neither tea nor coffee? SOLUTION Let the set of students who were taking tea be T and let the set of students who were taking coffee be C. The 600 students who took part in the survey form the universal set denoted by U. n (U) = 600 n (T) = 150 n (C) = 225 n (T ∩ C) = 100 We know that n (T ∪ C) = n (T) + n (C) - n (T ∩ C) = 150 + 225 - 100 n (T ∪ C) = 275 Number of students who are not taking either tea or coffee = Total number of students - Number of students who are taking either tea or coffee n (T' ∩ C')= n (U) - n (T ∪ C) = 600 - 275 = 325 Hence, number of students who take neither tea nor coffee = 325 14. In a group of students, 100 students know Hindi, 50 know English and 25 know both. Each of the students knows either Hindi or English. How many students are there in the group? SOLUTION Let the set with all students in the group be U. Let the set of students who know Hindi be X and those who know English be Y. n (X) = 100 n (Y) = 50 n (X ∩ Y) = 25 n (X ∪ Y) = n (U) (Given) We know that n (X ∪ Y) = n (X) + n (Y) - n (X ∩ Y) = 100 + 50 - 25 = 125 Hence, there were a total of 125 students in the group. 15. In a survey of 60 people, it was found that 25 people read newspaper H, 26 read newspaper T, 26 read newspaper I, 9 read both H and I, 11 read both H and T, 8 read both T and I, 3 read all three newspapers. Find:
SOLUTION Let the set of people who read newspaper H be A, those who read T be B and those who read I be C. n (A) = 25 n (B) = 26 n (C) = 26 n (A ∩ C) = 9 n (B ∩ C) = 8 n (A ∩ B) = 11 n (A ∩ B ∩ C) = 3 (i) We know that n (A ∪ B ∪ C) = n (A) + n (B) + n (C) - n (A ∩ B) - n (B ∩ C) - n (A ∩ C) + n (A ∩ B ∩ C) = 25 + 26 + 26 - 9 - 8 - 11 + 3 = 52 Hence, there are 52 people who read at least one newspaper. (ii) n (A ∩ B) = People who read H and T only + People who read all three n (B ∩ C) = People who read H and I only + People who read all three n (A ∩ C) = People who read I and T only + People who read all three Add all three n (A ∩ B) + n (B ∩ C) + n (A ∩ C) = Number of people who read more than one newspaper + 2 × n (A ∩ B ∩ C) 11 + 8 + 9 = Number of people who read more than one newspaper + 6 Number of people who read more than one newspaper = 22 Number of people who read only one newspaper = 52 - 22 = 30 Hence, 30 people read exactly one newspaper. 16. In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only. SOLUTION n (A) = 21 n (B) = 26 n (C) = 29 n (A ∩ B) = 14 n(C ∩ A) = 12 n (B ∩ C) = 14 n (A ∩ B ∩ C) = 8 We need to draw the venn diagram. 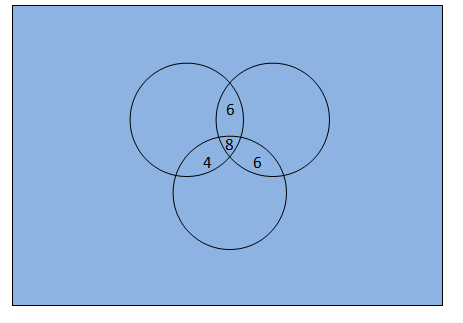 Number of people who only like product C = 29 - (4 + 8 + 6) = 11 Hence, 11 people like product C only. Next TopicClass 11 Maths Chapter 2 |