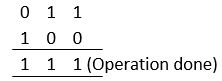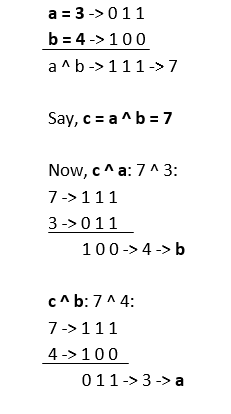Python Bitwise XOR Operator

Binary language is the language of a computer. All the inner mechanisms of a computer happen concerning bits. Bitwise operators are the set of operators that allow the programmer to perform bitwise operations on integers. These operators allow the programmer to manipulate the lower-level data in a computer. There are a total of six bitwise operators in Python:

1. Bitwise AND
2. Bitwise OR
3. Bitwise NOT
4. Bitwise XOR
5. Bitwise right shift
6. Bitwise left shift

This article discusses the Bitwise XOR operator with examples.

• When we apply a bitwise operator on two operands, the integer values are converted into their binary forms-into bits.
• Then, the operator performs the operation bit-by-bit on every individual bit.
• After the operation, the binary number is converted to decimal form and returned as the output.

Now, let us understand the operation of Bitwise XOR:

• It is called "Exclusive OR". It excludes the 1 | 1 -> 1 condition from 'or'.
• It is a binary operator - performed between two operands.
• Representation: a ^ b where 'a' and 'b' are two operands.
• Return value: It returns an integer when performed between two integers and a Boolean value when performed between two Boolean values.

Operation:

1. The given two integers are converted into binary form.
2. In the two binary notations:

• If both corresponding bits are the same - (1 ^ 1), (0 ^ 0), it returns 0.
• If both corresponding bits are different - (1 ^ 0), (0 ^ 1), it returns 1.

The truth table of XOR:

Let us understand the concept using an example:

If we want to perform:

3 ^ 4:

1. Both the integers are converted into binary forms:

3 -> 0 1 1

4 -> 1 0 0

2. Now, xor is applied bitwise: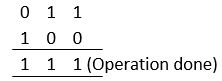

3. Finally, the resultant binary number is converted back to its decimal form.

1 1 1 represents 7

4. Output -> 7

3 ^ 4 -> 7

Now, for the same operands, let us write a code for xor:

Output: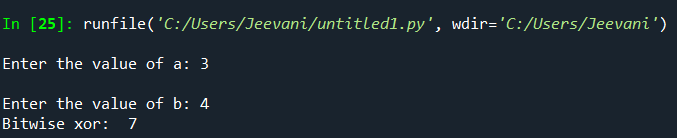

On Boolean values:

We can perform xor on Boolean values. When we operate on two integers, 1 is equivalent to Boolean True, and 0 is equivalent to Boolean False.

Truth table:

Output:

Structure of outputs:

• If we performed xor on a and b -> a ^ b. As a result, we got some integer c (a ^ b -> c) then,

1. If we perform xor on c and a, b will be the output -> c ^ a -> b
2. If we perform xor on c and b, a will be the output -> c ^ b -> a

Let us take the above example: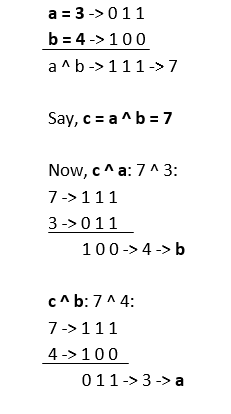

Code:

Output: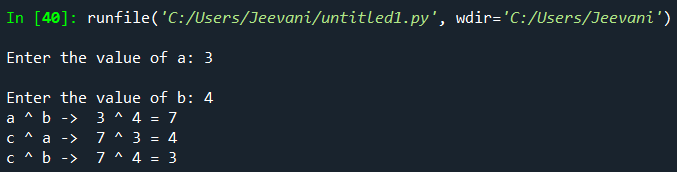

Understanding:

If a ^ b -> c

Then,

c ^ a -> b

c ^ b -> a

• If we know the output and one operand, we can find the other operand using this relation.
• This relation is only possible with xor because of its truth table.

Role of xor in cryptography:

The above relation got xor a small role in cryptography models.

• If a person 'A' wants to send a numerically encoded message to another person 'B' confidentially, he needs one more simple cover for the encoded message.
• Both A and B will have a secret key known to each other beforehand.
• Now, A will XOR the message with the secret key and send it to B.
• After receiving, B can perform xor again with the received xor result and secret key and get the message.

Example:

If A wants to send the message 3 to B and their secret key is 4

3 ^ 4 -> 5.

A will send 5 to B.

B already knows the secret key is 4.

He will decrypt the message using xor again:

5 ^ 4 -> 3

Message successfully received.

• This method is the simplest, and so is the weakest cryptography method.