Quick Sort Algorithm

In this article, we will discuss the Quicksort Algorithm. The working procedure of Quicksort is also simple. This article will be very helpful and interesting to students as they might face quicksort as a question in their examinations. So, it is important to discuss the topic.

Sorting is a way of arranging items in a systematic manner. Quicksort is the widely used sorting algorithm that makes n log n comparisons in average case for sorting an array of n elements. It is a faster and highly efficient sorting algorithm. This algorithm follows the divide and conquer approach. Divide and conquer is a technique of breaking down the algorithms into subproblems, then solving the subproblems, and combining the results back together to solve the original problem.

Divide: In Divide, first pick a pivot element. After that, partition or rearrange the array into two sub-arrays such that each element in the left sub-array is less than or equal to the pivot element and each element in the right sub-array is larger than the pivot element.

Conquer: Recursively, sort two subarrays with Quicksort.

Combine: Combine the already sorted array.

Quicksort picks an element as pivot, and then it partitions the given array around the picked pivot element. In quick sort, a large array is divided into two arrays in which one holds values that are smaller than the specified value (Pivot), and another array holds the values that are greater than the pivot.

After that, left and right sub-arrays are also partitioned using the same approach. It will continue until the single element remains in the sub-array.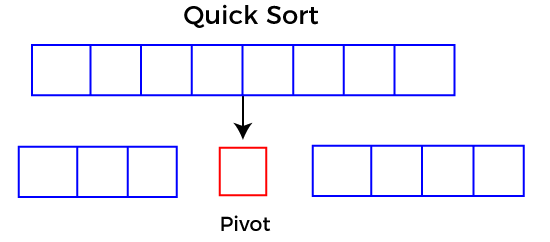

Choosing the pivot

Picking a good pivot is necessary for the fast implementation of quicksort. However, it is typical to determine a good pivot. Some of the ways of choosing a pivot are as follows -

Pivot can be random, i.e. select the random pivot from the given array.
Pivot can either be the rightmost element of the leftmost element of the given array.
Select median as the pivot element.

Algorithm

Algorithm:

QUICKSORT (array A, start, end)   
{
 1 if (start < end)   
 2 {
3 p = partition(A, start, end)
4 QUICKSORT (A, start, p - 1)  
5 QUICKSORT (A, p + 1, end)  
6 } 
}

Partition Algorithm:

The partition algorithm rearranges the sub-arrays in a place.

PARTITION (array A, start, end)   
{
pivot ? A[end]   
i ? start-1   
for j ? start to end -1 {
do if (A[j] < pivot) {  
then i ? i + 1   
swap A[i] with A[j] 
}} 
swap A[i+1] with A[end]   
return i+1
}

Working of Quick Sort Algorithm

Now, let's see the working of the Quicksort Algorithm.

To understand the working of quick sort, let's take an unsorted array. It will make the concept more clear and understandable.

Let the elements of array are -

In the given array, we consider the leftmost element as pivot. So, in this case, a[left] = 24, a[right] = 27 and a[pivot] = 24.

Since, pivot is at left, so algorithm starts from right and move towards left.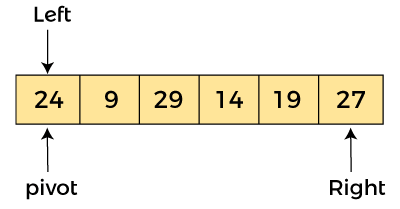

Now, a[pivot] < a[right], so algorithm moves forward one position towards left, i.e. -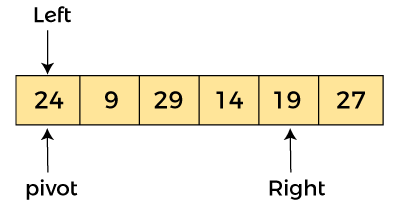

Now, a[left] = 24, a[right] = 19, and a[pivot] = 24.

Because, a[pivot] > a[right], so, algorithm will swap a[pivot] with a[right], and pivot moves to right, as -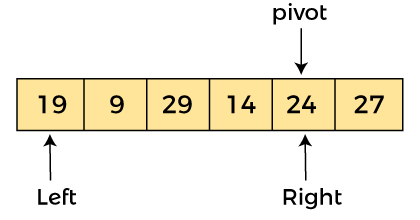

Now, a[left] = 19, a[right] = 24, and a[pivot] = 24. Since, pivot is at right, so algorithm starts from left and moves to right.

As a[pivot] > a[left], so algorithm moves one position to right as -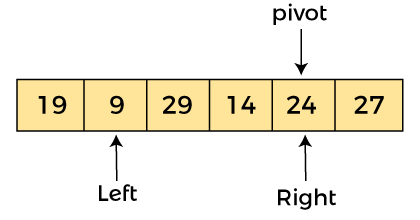

Now, a[left] = 9, a[right] = 24, and a[pivot] = 24. As a[pivot] > a[left], so algorithm moves one position to right as -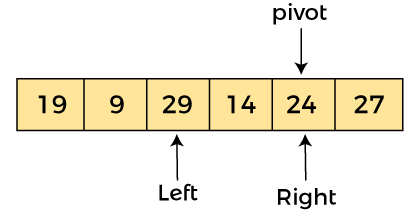

Now, a[left] = 29, a[right] = 24, and a[pivot] = 24. As a[pivot] < a[left], so, swap a[pivot] and a[left], now pivot is at left, i.e. -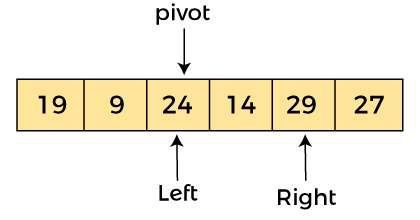

Since, pivot is at left, so algorithm starts from right, and move to left. Now, a[left] = 24, a[right] = 29, and a[pivot] = 24. As a[pivot] < a[right], so algorithm moves one position to left, as -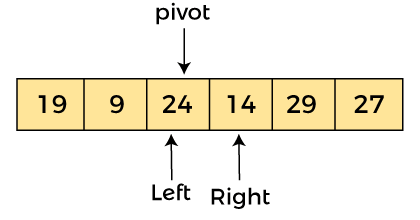

Now, a[pivot] = 24, a[left] = 24, and a[right] = 14. As a[pivot] > a[right], so, swap a[pivot] and a[right], now pivot is at right, i.e. -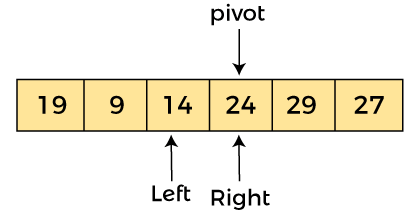

Now, a[pivot] = 24, a[left] = 14, and a[right] = 24. Pivot is at right, so the algorithm starts from left and move to right.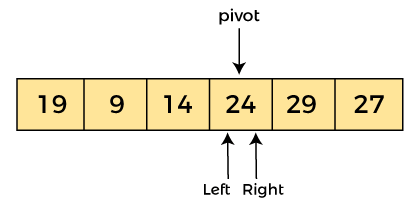

Now, a[pivot] = 24, a[left] = 24, and a[right] = 24. So, pivot, left and right are pointing the same element. It represents the termination of procedure.

Element 24, which is the pivot element is placed at its exact position.

Elements that are right side of element 24 are greater than it, and the elements that are left side of element 24 are smaller than it.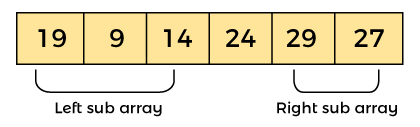

Now, in a similar manner, quick sort algorithm is separately applied to the left and right sub-arrays. After sorting gets done, the array will be -

Quicksort complexity

Now, let's see the time complexity of quicksort in best case, average case, and in worst case. We will also see the space complexity of quicksort.

1. Time Complexity

Case	Time Complexity
Best Case	O(n*logn)
Average Case	O(n*logn)
Worst Case	O(n²)

Best Case Complexity - In Quicksort, the best-case occurs when the pivot element is the middle element or near to the middle element. The best-case time complexity of quicksort is O(n*logn).
Average Case Complexity - It occurs when the array elements are in jumbled order that is not properly ascending and not properly descending. The average case time complexity of quicksort is O(n*logn).
Worst Case Complexity - In quick sort, worst case occurs when the pivot element is either greatest or smallest element. Suppose, if the pivot element is always the last element of the array, the worst case would occur when the given array is sorted already in ascending or descending order. The worst-case time complexity of quicksort is O(n²).

Though the worst-case complexity of quicksort is more than other sorting algorithms such as Merge sort and Heap sort, still it is faster in practice. Worst case in quick sort rarely occurs because by changing the choice of pivot, it can be implemented in different ways. Worst case in quicksort can be avoided by choosing the right pivot element.

2. Space Complexity

Space Complexity	O(n*logn)
Stable	NO

The space complexity of quicksort is O(n*logn).

Implementation of quicksort

Now, let's see the programs of quicksort in different programming languages.

Program: Write a program to implement quicksort in C language.

#includ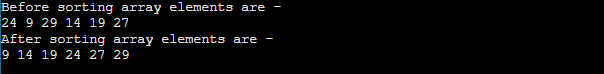e <stdio.h>
/* function that consider last element as pivot, 
place the pivot at its exact position, and place 
smaller elements to left of pivot and greater 
elements to right of pivot.  */
int partition (int a[], int start, int end)
{
	int pivot = a[end]; // pivot element
	int i = (start - 1);

	for (int j = start; j <= end - 1; j++)
	{
		// If current element is smaller than the pivot
		if (a[j] < pivot)
		{
			i++; // increment index of smaller element
			int t = a[i];
			a[i] = a[j];
			a[j] = t;
		}
	}
	int t = a[i+1];
	a[i+1] = a[end];
	a[end] = t;
	return (i + 1);
}

/* function to implement quick sort */
void quick(int a[], int start, int end) /* a[] = array to be sorted, start = Starting index, end = Ending index */
{
	if (start < end)
	{
		int p = partition(a, start, end); //p is the partitioning index
		quick(a, start, p - 1);
		quick(a, p + 1, end);
	}
}

/* function to print an array */
void printArr(int a[], int n)
{
	int i;
	for (i = 0; i < n; i++)
		printf("%d ", a[i]);
}
int main()
{
	int a[] = { 24, 9, 29, 14, 19, 27 };
	int n = sizeof(a) / sizeof(a[0]);
    printf("Before sorting array elements are - \n");
    printArr(a, n);
    quick(a, 0, n - 1);
    printf("\nAfter sorting array elements are - \n");  
    printArr(a, n);
    
	return 0;
}

Output:

Program: Write a program to implement quick sort in C++ language.

#include <iostream>

using namespace std;

/* function that consider last element as pivot, 
place the pivot at its exact position, and place 
smaller elements to left of pivot and greater 
elements to right of pivot.  */
int partition (int a[], int start, int end)
{
	int pivot = a[end]; // pivot element
	int i = (start - 1);

	for (int j = start; j <= end - 1; j++)
	{
		// If current element is smaller than the pivot
		if (a[j] < pivot)
		{
			i++; // increment index of smaller element
			int t = a[i];
			a[i] = a[j];
			a[j] = t;
		}
	}
	int t = a[i+1];
	a[i+1] = a[end];
	a[end] = t;
	return (i + 1);
}

/* function to implement quick sort */
void quick(int a[], int start, int end) /* a[] = array to be sorted, start = Starting index, end = Ending index */
{
	if (start < end)
	{
		int p = partition(a, start, end);  //p is the partitioning index
		quick(a, start, p - 1);
		quick(a, p + 1, end);
	}
}

/* function to print an array */
void printArr(int a[], int n)
{
	int i;
	for (i = 0; i < n; i++)
	    cout<<a[i]<< " ";
}
int main()
{
	int a[] = { 23, 8, 28, 13, 18, 26 };
	int n = sizeof(a) / sizeof(a[0]);
    cout<<"Before sorting array elements are - \n";
    printArr(a, n);
    quick(a, 0, n - 1);
    cout<<"\nAfter sorting array elements are - \n";  
    printArr(a, n);
    
	return 0;
}

Output:

Program: Write a program to implement quicksort in python.

#function that consider last element as pivot, 
#place the pivot at its exact position, and place 
#smaller elements to left of pivot and greater 
#elements to right of pivot. 

def partition (a, start, end):
	i = (start - 1)
	pivot = a[end] # pivot element
	
	for j in range(start, end):
		# If current element is smaller than or equal to the pivot
		if (a[j] <= pivot):
		    i = i + 1
		    a[i], a[j] = a[j], a[i]
	
	a[i+1], a[end] = a[end], a[i+1]

	return (i + 1)
	
# function to implement quick sort 
def quick(a, start, end): # a[] = array to be sorted, start = Starting index, end = Ending index  	
	if (start < end):
		p = partition(a, start, end) # p is partitioning index
		quick(a, start, p - 1)
		quick(a, p + 1, end)

		
def printArr(a): # function to print the array
    for i in range(len(a)):
	    print (a[i], end = " ")

	
a = [68, 13, 1, 49, 58]
print("Before sorting array elements are - ")
printArr(a)
quick(a, 0, len(a)-1)
print("\nAfter sorting array elements are - ")
printArr(a)

Output:

Program: Write a program to implement quicksort in Java.

public class Quick
{
    /* function that consider last element as pivot, 
place the pivot at its exact position, and place 
smaller elements to left of pivot and greater 
elements to right of pivot.  */
int partition (int a[], int start, int end)
{
	int pivot = a[end]; // pivot element
	int i = (start - 1);

	for (int j = start; j <= end - 1; j++)
	{
		// If current element is smaller than the pivot
		if (a[j] < pivot)
		{
			i++; // increment index of smaller element
			int t = a[i];
			a[i] = a[j];
			a[j] = t;
		}
	}
	int t = a[i+1];
	a[i+1] = a[end];
	a[end] = t;
	return (i + 1);
}

/* function to implement quick sort */
void quick(int a[], int start, int end) /* a[] = array to be sorted, start = Starting index, end = Ending index */
{
	if (start < end)
	{
		int p = partition(a, start, end);  //p is partitioning index
		quick(a, start, p - 1);
		quick(a, p + 1, end);
	}
}

/* function to print an array */
void printArr(int a[], int n)
{
	int i;
	for (i = 0; i < n; i++)
	    System.out.print(a[i] + " ");
}
	public static void main(String[] args) {
	int a[] = { 13, 18, 27, 2, 19, 25 };
	int n = a.length;
    System.out.println("\nBefore sorting array elements are - ");
    Quick q1 = new Quick();
    q1.printArr(a, n);
    q1.quick(a, 0, n - 1);
    System.out.println("\nAfter sorting array elements are - ");
    q1.printArr(a, n);
    System.out.println();
	}
}

Output

After the execution of above code, the output will be -

Program: Write a program to implement quick sort in php.

<?php  
    /* function that consider last element as pivot, 
place the pivot at its exact position, and place 
smaller elements to left of pivot and greater 
elements to right of pivot.  */
function partition (&$a, $start, $end)
{
	$pivot = $a[$end]; // pivot element
	$i = ($start - 1);

	for ($j = $start; $j <= $end - 1; $j++)
	{
		// If current element is smaller than the pivot
		if ($a[$j] < $pivot)
		{
			$i++; // increment index of smaller element
			$t = $a[$i];
			$a[$i] = $a[$j];
			$a[$j] = $t;
		}
	}
	$t = $a[$i+1];
	$a[$i+1] = $a[$end];
	$a[$end] = $t;
	return ($i + 1);
}

/* function to implement quick sort */
function quick(&$a, $start, $end) /* a[] = array to be sorted, start = Starting index, end = Ending index */
{
	if ($start < $end)
	{
		$p = partition($a, $start, $end); //p is partitioning index
		quick($a, $start, $p - 1);
		quick($a, $p + 1, $end);
	}
}

    function printArray($a, $n)
    {
    for($i = 0; $i < $n; $i++)  
    {  
        print_r($a[$i]);  
        echo " ";  
    }      
    }
	$a = array( 89, 47, 2, 17, 8, 19 );  
	$n = count($a);
    echo "Before sorting array elements are - <br>";  
    printArray($a, $n);
    quick($a, 0, $n - 1);
    echo "<br> After sorting array elements are - <br>";  
    printArray($a, $n);
    
?>

Output

After the execution of above code, the output will be -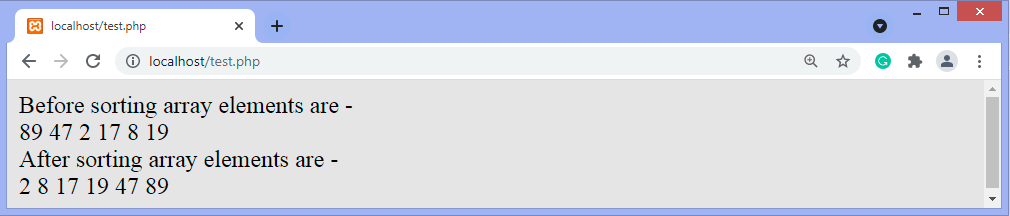

So, that's all about the article. Hope the article will be helpful and informative to you.

This article was not only limited to the algorithm. Along with the algorithm, we have also discussed the quick sort complexity, working, and implementation in different programming languages.

Next TopicRadix Sort

← prev next →