Recursive Descent Parser

A top-down parser is known as a recursive descent parser that analyses input based on grammar rules using recursive methods. Starting with the grammar's topmost rule, the parser executes subroutines backward for each input symbol that is not a terminal symbol until it reaches one. A parse tree representing the input's structure according to the grammar is the parser's output.

Recursive Parser Descent:

The process of parsing is frequently employed in language processing and compiler design. It is founded on the idea that a difficult problem can be broken down into simpler problems and then solved recursively. Starting with a top-level nonterminal symbol, the parsing process proceeds by recursively expanding nonterminals until it reaches terminal symbols.

Repeated descent, the fundamental idea behind parsing is to create a set of parsing functions, each of which corresponds to a nonterminal grammar symbol. These procedures are responsible for locating and assessing the relevant linguistic components. The top-level function is called first by the parser, which then calls the necessary parsing routines recursively depending on the structure of the input.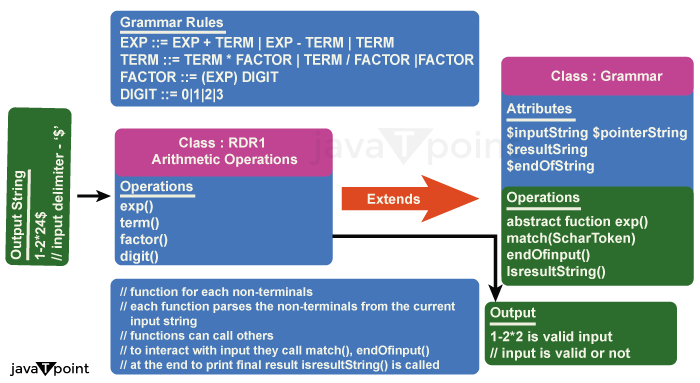

Grammar:

Defining the grammar of the language to be parsed is the first stage in developing a recursive descent parser. A collection of rules known as grammar define the syntax of a language. Each rule is made up of a series of terminal and nonterminal symbols on the right side and a nonterminal symbol on the left side.

Take the grammar for a straightforward arithmetic language, for instance:

expression ::= term ( '+' term | '-' term )*
term       ::= factor ( '*' factor | '/' factor )*
factor     ::= '(' expression ')' | number
number     ::= [0-9]+

Expression, term, factor, and number are the grammar's four nonterminal symbols. An arithmetic expression is defined as one or more terms divided by plus or minus signs by the expression rule, which serves as the foundation for parsing. According to the term rule, a term is defined as one or more factors divided by multiplication or division signs. A number or an expression surrounded in brackets is what the factor rule refers to as a factor. As per the number rule, a number consists of one or more digits.

Parsing:

The fundamental principle of recursive descent is Writing a collection of recursive functions, one for each nonterminal symbol in the grammar, is the process of parsing. A series of symbols that matches a particular rule must be parsed by each function, which is assigned to a grammar rule.

The expression function, which is invoked with the input string, is where the recursive descent parser begins. Depending on whether the symbol is a number or an opening parenthesis, the function analyses the first symbol of the input and chooses which alternative of the term rule to apply. The factor function is used to parse the symbol's value if it is a number. The expression function is used recursively to parse the expression inside the parentheses if the symbol is an opening parenthesis. The term function is invoked recursively to parse any subsequent multiplication or division signs and factors after the factor or expression function has returned.

The expression function determines whether there are any plus or minus signs after the term if the term function returns a value. If so, the term function is invoked once more to parse the subsequent term. Until an error happens or all of the input has been parsed, this procedure continues.

Say, for instance, that we want to parse the formula 2 + 3 * (4 - 1) / 2. This is how the recursive descent parser operates:

expression("2 + 3 * (4 - 1) / 2")
  term("2")
  term("+ 3 * (4 - 1) / 2")
    factor("3")
    factor("* (4 - 1) / 2")
      term("(4 - 1)")
        factor("4")
        factor("- 1")
          factor("1")
      term("/ 2")
        factor("2")

The parser first calls the expression function with the supplied string. When "2" is provided as input, the function calls another function, which then executes the data and returns. The expression function then reads the next symbol, a plus sign. It again calls the term function with the input ",".

Recursive descent parsing has the following benefits:

Ease of use: Because recursive descent parsing closely mimics the grammar rules of the language being parsed, it is simple to comprehend and use.
Readability: The parsing code is usually set up in a structured and modular way, which makes it easier to read and maintain.
Recursive descent parsers can produce descriptive error messages, which make it simpler to find and detect syntax mistakes in the input. 3. Error reporting.
Predictability: The predictable behavior of recursive descent parsers makes the parsing process deterministic and clear.

Recursive descent parsing, however, also has certain drawbacks:

Recursive descent parsers encounter difficulties with left-recursive grammar rules since they can result in unbounded recursion. To effectively handle left recursion, care must be made to avoid it or employ methods like memoization.
Recursive descent parsers rely on backtracking when internal alternatives to a grammar rule are unsuccessful. This could result in inefficiencies, especially if the grammar contains a lot of ambiguity or options.
Recursive descent parsers frequently adhere to the LL(1) constraint, which requires that they only use one token of lookahead. The grammar's expressiveness is constrained by this restriction because it is unable to handle some ambiguous or context-sensitive languages.

An outline of the Recursive Descent Parsing algorithm is provided below:

Grammar: The first step in parsing a language is to define its grammar. A set of production rules that outline the language's syntactic structure makes up the grammar. Each rule is made up of a series of terminal and nonterminal symbols on the right side and a nonterminal symbol on the left side.
Create parsing functions: For each nonterminal symbol in the grammar, create a parsing function. The task of identifying and parsing the linguistic expressions corresponding to each nonterminal symbol will fall to each function.
Input tokens read: Read the input tokens that came from the tokenizer or lexical analyzer. The IDs, keywords, operators, and other components of the input language are represented by these tokens.
Implement parsing functions: Recursively implement each parsing function. These steps should be followed by each function:
1. Verify if the current token matches the nonterminal's anticipated symbol.
2. If the nonterminal has numerous production rules, handle each alternative using an if-else or switch statement. Each possibility ought to be represented by a different function call or block of code.
3. Recursively invoke the parsing routines for each alternative's matching nonterminals in the rule. The parsing procedure will continue until all of the input has been processed thanks to this recursive call.
4. Take care of any additional nonterminal-specific logic, such as parse tree construction or semantic actions.
Start parsing: Launch the parsing operation by invoking the parsing function that corresponds to the grammar's start symbol. The recursive descent parsing procedure will get started with this function.
Implement error-handling procedures to handle unusual input or notify syntax mistakes. Give the user clear error messages when one happens so they may comprehend and fix the issue.

The Recursive Descent Parsing algorithm can be used to parse a given language by its grammatical rules by carrying out the stages listed below.

Implementation of Code:

INTEGER = 'INTEGER'
PLUS = 'PLUS'
MINUS = 'MINUS'
MULTIPLY = 'MULTIPLY'
DIVIDE = 'DIVIDE'
LPAREN = 'LPAREN'
RPAREN = 'RPAREN'
EOF = 'EOF'

class Token:
    def __init__(self, type1, value1):
        self.type1 = type1
        self.value1 = value1

class Lexer:
    def __init__(self, t):
        self.text = t
        self.pos = 0
        self.current_char = self.text[self.pos]

    def error(self):
        raise Exception('Invalid character')

    def advance(self):
        self. pos += 1
        if self.pos >= len(self.text):
            self.current_char = None
        else:
            self.current_char = self.text[self.pos]

    def integer(self):
        result = ''
        while self.current_char is not None and self.current_char.isdigit():
            result += self.current_char
            self.advance()
        return int(result)

    def get_next_token(self):
        while self.current_char is not None:
            if self.current_char.isspace():
                self.advance()
                continue
            elif self.current_char.isdigit():
                return Token(INTEGER, self.integer())
            elif self.current_char == '+':
                self.advance()
                return Token(PLUS, '+')
            elif self.current_char == '-':
                self.advance()
                return Token(MINUS, '-')
            elif self.current_char == '*':
                self.advance()
                return Token(MULTIPLY, '*')
            elif self.current_char == '/':
                self.advance()
                return Token(DIVIDE, '/')
            elif self.current_char == '(':
                self.advance()
                return Token(LPAREN, '(')
            elif self.current_char == ')':
                self.advance()
                return Token(RPAREN, ')')
            else:
                self.error()
        return Token(EOF, None)

class Parser:
    def __init__(self, lexer):
        self.lexer = lexer
        self.current_token = self.lexer.get_next_token()

    def error(self):
        raise Exception('Invalid syntax')

    def eat(self, token_type):
        if self.current_token.type == token_type:
            self.current_token = self.lexer.get_next_token()
        else:
            self.error()

    def factor(self):
        token = self.current_token
        if token.type == INTEGER:
            self.eat(INTEGER)
            return token.value
        elif token.type == LPAREN:
            self.eat(LPAREN)
            result = self.expr()
            self.eat(RPAREN)
            return result

    def term(self):
        result = self.factor()
        while self.current_token.type in (MULTIPLY, DIVIDE):
            token = self.current_token
            if token.type == MULTIPLY:
                self.eat(MULTIPLY)
                result *= self.factor()
            elif token.type == DIVIDE:
                self.eat(DIVIDE)
                result /= self.factor()
        return result

    def expr(self):
        result = self.term()
        while self.current_token.type in (PLUS, MINUS):
            token = self.current_token
            if token.type == PLUS:
                self.eat(PLUS)
                result += self.term()
            elif token.type == MINUS:
                self.eat(MINUS)
                result -= self.term()
        return result

    def parse(self):
        return self.expr()

def main():
    while True:
        try:
            text = input('Enter an arithmetic expression: ')
        except EOFError:
            break
        lexer = Lexer(text)
        parser = Parser(lexer)
        result = parser.parse()
        print(result)
main()

Output:

The given code implements a simple calculator application that evaluates arithmetic expressions.

The code defines several token kinds, such as INTEGER, PLUS, MINUS, MULTIPLY, DIVIDE, LPAREN, RPAREN, and EOF. These token types serve as representations for the various elements of the input expression.
A token is represented by a straightforward data structure called the Token class. It contains two attributes: value to record the relevant value and type to hold the token type.
The input text is tokenized by the Lexer class. Character by character, it reads the text, locating tokens, and sending them back to the parser.
The advance() method advances the input text to the following character.
Using the input text, the integer() method extracts a series of digits and returns the matching integer value.
The lexer's primary function is the get_next_token() method. It looks through the text to find the current token before returning a Token object.
The main() method serves as the program's starting point.
It requests an equation from the user, then reads the input.
A Lexer object is created from the input text, and a Parser object is created from the Lexer.
It calls the parser's parse() method to parse the expression and determine the result.
After that, the result is printed.

Conclusion:

Recursive descent parsing is a key method in compiler design and parsing theory overall. It is a popular option for simple languages and educational reasons since it offers a simple and intuitive way of parsing. Anyone interested in language parsing and compiler development would benefit from understanding the fundamentals and practical use of recursive descent parsers.

Next Topic#

← prev next →