Zero matrix in Discrete mathematics

A matrix will be known as a zero matrix if all the elements of this matrix are equal to 0. Since a zero matrix is used to contain only zeros in the form of its elements. Therefore, it will also be known as the null matrix. In other words, the zero matrix was introduced so that it can represent nothing symbolically, and the word "null" is also used to show nothing. Hence, a zero matrix is also known as a null matrix. Sometimes, a zero matrix is also a square matrix.

When we add any other matrix to a null matrix, then it will result in the same matrix. Hence we can say that the null matrix is also known as the additive identity of a given matrix. The m∗n is known as the order of the null matrix, and this order can contain an unequal number of rows and columns. There are some examples of zero or null matrices, which are described as follows: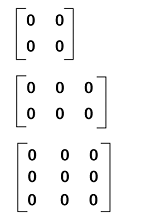

In this section, we will learn about the definition, examples, and properties of null matrices.

Definition of Zero matrix

A zero matrix can be described as an arrangement of zero elements in the form of rows and columns. A zero matrix is a kind of matrix in which all its entries is zero. With the help of symbol O, we can indicate the zero matrix or null matrix. We can express this matrix with a subscript to indicate the dimension of the matrix.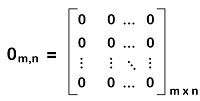

If there is a matrix and a zero matrix in the same order, then the addition of these matrices will not change the matrix. That's why this matrix is also known as the additive identity.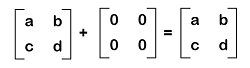

Examples of Zero matrices

Here we will show the zero matrices with different orders, which are described as follows:

1. This matrix is a zero matrix that contains the order 1∗1. We can see that this matrix contains one zero in the form of 1 row and 1 column.
   O = [0]
2. This matrix is a zero matrix that contains the order 1∗2. We can see that this matrix contains two zeros in the form of 1 row and 2 columns.
   O = [0 0]
3. This matrix is a zero matrix that contains the order 2∗2. We can see that this matrix contains four zeros in the form of 2 rows and 2 columns.
   
4. This matrix is a zero matrix that contains the order 3∗3. We can see that this matrix contains nine zeros in the form of 3 rows and 3 columns.

In the above examples, we have seen the formation of zero matrices in discrete mathematics. Through these, we have also cleared that a zero matrix can be a square matrix or rectangular matrix.

Note:

• In case of a zero matrix, all the entries are equal to zero.
• If there is a matrix A and a zero matrix, then we will get A as the output matrix.

Addition of Zero matrix

When we add a zero matrix and a non-zero matrix, which contains the same order m∗n, then the addition of these matrices will be the original matrix itself.

Suppose there is an m∗n matrix A where A = [aij] and a zero matrix O which is also an m∗n matrix. Then it will contain the following relation:

Examples of zero matrix

Here we will show examples of the additive matrices, which are described as follows: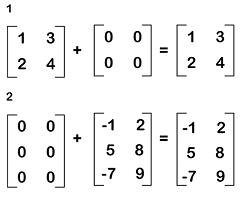

In these examples, we can see that when we add a zero matrix and another matrix, then in the resultant matrix, the identity of the matrix will not be changed. Therefore, it will be known as the additive identity for matrix addition.

Multiplication of zero matrix

Suppose there are two non-zero matrices. If we add these matrices, then it will be possible to get a zero matrix. If we have two real numbers, x and y, where xy = 0, in this case, either x = 0 or y = 0. In case of matrices, we can also apply the same concept. So if rows of matrix A are used to contain zero elements and the columns of matrix B are also used to contain the zero elements and both the matrices have the same order, in this case, then the multiplication of these matrices will be a zero matrix.

Example of multiplication of zero matrix

Suppose there are two non-zero matrices, A and B, which are described as follows: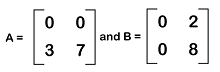

Solution: The multiplication of A and B will be equal to the following: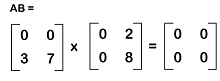

Note: If we get a zero matrix as the result of the multiplication of two matrices, then it will not be necessary that one of the matrices is a zero matrix.

Properties of zero matrix

There are a lot of important properties in the null matrix, which is described as follows:

• The null matrix can also be a square matrix.
• In the null matrix, there can be an unequal number in the form of rows and columns.
• The original matrix will not be changed in the resultant matrix when we add any matrix to a null matrix.
• The original matrix will be changed into the null matrix in the resultant matrix when we multiply any matrix by a null matrix.
• In case of a null matrix, the determinant will be equal to zero.
• The null matrix is a type of singular matrix.

Examples of zero matrix

There are a lot of examples of zero matrices, and some of them are described as follows:

Example 1: In this example, we have to show a null matrix that contains 2 rows and 3 columns.

Solution: If a null matrix is used to contain 2 rows and 3 columns, then it means that it will contain an order 2∗3. All the elements of this matrix will be 0.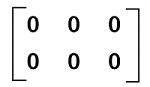

Thus, we get the required null matrix.

Example 2: In this example, we have an additive identity, and we have to show that the additive identity of this matrix is a null matrix. The additive identity is described as follows: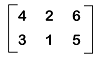

Solution: From the question, we have the following additive identity: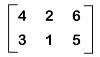

The null matrix with the same order is described as follows: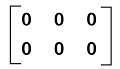

The addition of the given matrix and the null matrix is described as follows: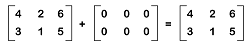

Hence we can see that the addition of the given matrix and the null matrix provides us the same matrix.

Therefore, it is proved that the null matrix is the additive identity of the above matrix.